Bài viết

Giải Sudoku bằng thuật toán quay lui

Đăng lúc Cập nhật lúc
14 phút đọc

Bài này mình viết về thuật toán backtracking (quay lui) của bài toán giải Sudoku. Sau đó sẽ bàn thêm về một số đặc điểm, trường hợp nào backtracking xử lý tệ nhất.

Giới thiệu

Vì ô chữ số Sudoku cũng khá là quen thuộc rồi nên mình cũng không giới thiệu nhiều nữa. Chỉ note 2

  • Sudoku là ô chữ số có dạng lưới 9x9 ô
    • dạng tổng quát là $n^2 \times n^2$ ô (Không tính đến các biến thể khác như 6x6)
  • Mỗi hàng, mỗi cột, và mỗi ô 3x3 nhỏ phải chứa các số từ 1 đến 9 và không có số trùng nhau
    • (thực ra nếu có số trùng thì cũng không điền đủ các số từ 1 đến 9 được)
    • tương tự, thì dạng tổng quát là điền các số từ 1 đến $n$ vào các hàng, cột, và ô $n \times n$ nhỏ

Hiển thị Sudoku trong Python

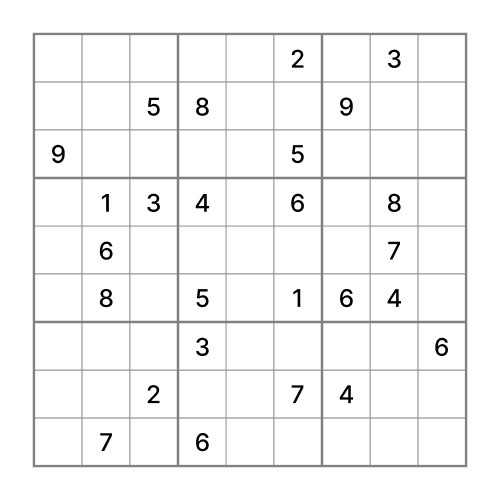
Trước khi giải thì cần xem xét làm sao để nhập trước. Giả sử chúng ta có câu đố Sudoku trên trang WebSudoku như sau:

Sudoku Example light Sudoku Example dark

Thường thì các ô Sudoku sẽ được input ở dạng array 9x9:

1
2
3
4
5
6
7
8
9

sudoku_grid = [[0, 0, 0, 0, 0, 2, 0, 3, 0],
               [0, 0, 5, 8, 0, 0, 9, 0, 0],
               [9, 0, 0, 0, 0, 5, 0, 0, 0],
               [0, 1, 3, 4, 0, 6, 0, 8, 0],
               [0, 6, 0, 0, 0, 0, 0, 7, 0],
               [0, 8, 0, 5, 0, 1, 6, 4, 0],
               [0, 0, 0, 3, 0, 0, 0, 0, 6],
               [0, 0, 2, 0, 0, 7, 4, 0, 0],
               [0, 7, 0, 6, 0, 0, 0, 0, 0]]

Input như vậy thì cũng đã đủ để bắt tay vào giải rồi. Nhưng để dễ nhìn kết quả, chúng ta có thể tạo một hàm hiển thị sudoku đơn giản như sau

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

def display_sudoku(grid, blank_notation = "-"):
    for row in range(9):

        # In thêm dòng ngăn cách nếu ở các dòng 3, 6
        if row in (3,6):
            print("------+-------+------")

        # In thêm | để chia cột nếu ở các cột 3, 6
        for col in range(9):
            if col in (3,6):
                print("| ", end="")

            # Nếu là số 0, tức là giá trị chưa được điền
            # thì đổi thành blank_notation tuỳ ý
            number = grid[row][col]
            if number == 0:
                number = blank_notation

            # Viết số trong mảng, thêm khoảng cách " " phía sau
            print(number, end = " ")
        print()

sudoku_grid = [[0, 0, 0, 0, 0, 2, 0, 3, 0],
               [0, 0, 5, 8, 0, 0, 9, 0, 0],
               [9, 0, 0, 0, 0, 5, 0, 0, 0],
               [0, 1, 3, 4, 0, 6, 0, 8, 0],
               [0, 6, 0, 0, 0, 0, 0, 7, 0],
               [0, 8, 0, 5, 0, 1, 6, 4, 0],
               [0, 0, 0, 3, 0, 0, 0, 0, 6],
               [0, 0, 2, 0, 0, 7, 4, 0, 0],
               [0, 7, 0, 6, 0, 0, 0, 0, 0]]
display_sudoku(sudoku_grid, blank_notation=".")

Output

1
2
3
4
5
6
7
8
9
10
11

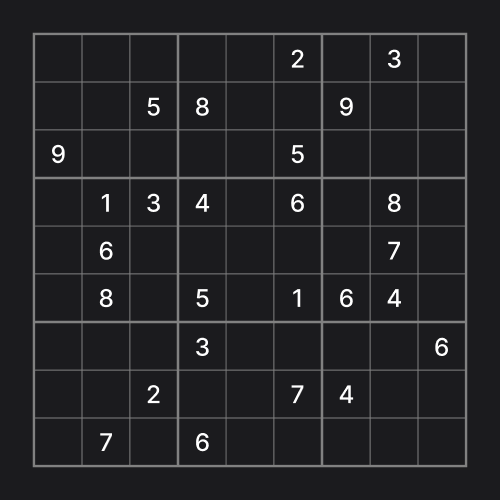
. . . | . . 2 | . 3 . 
. . 5 | 8 . . | 9 . . 
9 . . | . . 5 | . . . 
------+-------+------
. 1 3 | 4 . 6 | . 8 . 
. 6 . | . . . | . 7 . 
. 8 . | 5 . 1 | 6 4 . 
------+-------+------
. . . | 3 . . | . . 6 
. . 2 | . . 7 | 4 . . 
. 7 . | 6 . . | . . .

Ở đây mình có để giá trị blank_notation để tiện cho việc quan sát. Ta có thể thử tuỳ chỉnh thành các cách ghi khác, tuy nhiên chỉ sử dụng 1 ký tự thôi.

Input

1

display_sudoku(sudoku_grid, blank_notation=0)

Output

1
2
3
4
5
6
7
8
9
10
11

0 0 0 | 0 0 2 | 0 3 0 
0 0 5 | 8 0 0 | 9 0 0 
9 0 0 | 0 0 5 | 0 0 0 
------+-------+------
0 1 3 | 4 0 6 | 0 8 0 
0 6 0 | 0 0 0 | 0 7 0 
0 8 0 | 5 0 1 | 6 4 0 
------+-------+------
0 0 0 | 3 0 0 | 0 0 6 
0 0 2 | 0 0 7 | 4 0 0 
0 7 0 | 6 0 0 | 0 0 0

Xét điều kiện để điền giá trị

Dựa theo luật chơi của Sudoku, ta có:

  • Trong hàng không có giá trị trùng lặp
  • Trong cột không có giá trị trùng lặp
  • Trong ô 3x3 không có giá trị trùng lặp

Vậy ta có thể viết hàm để kiểm tra 3 điều kiện trên, và trả về False nếu đã tồn tại giá trị ở hàng, cột, hoặc ô 3x3 rồi, còn lại thì trả về True báo hiệu rằng có thể điền giá trị vào vị trí đang check.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

def can_input(grid, value, row, col):
    # Kiểm tra xem trong hàng muốn nhập đã có giá trị này chưa
    for i in range(9):
        if grid[row][i] == value:
            return False
        
    # Kiểm tra xem trong cột muốn nhập đã có giá trị này chưa
    for i in range(9):
        if grid[i][col] == value:
            return False

    # Xác định vị trí ô 3x3 nhỏ chứa vị trí muốn điền
    small_row = (row//3)*3
    small_col = (col//3)*3

    # Kiểm tra toàn bộ 9 ô trong mảng 3x3 xem đã có giá trị này chưa
    for i in range(3):
        for j in range(3):
            if grid[small_row + i][small_col + j] == value:
                return False

    # Nếu chưa có ở đâu hết thì có thể điền value
    return True

Giải Sudoku bằng thuật toán quay lui

Hàm quay lui thực ra là một trong những thuật toán brute-force (thử tất cả các biến cho đến khi tìm được kết quả).

Hàm này sẽ:

  • Check từ hàng đầu đến cuối, trái qua phải
  • Nếu thấy trống thì thử các số từ 1 đến 9 xem có hợp lý không.
    -> Đây chính là lý do chúng ta có hàm can_input ở trên để kiểm tra điều kiện.
  • Sau khi điền xong, hàm sẽ tiếp tục tiến tới ô tiếp theo và tiếp tục thử.
    • Nếu không thể tìm được số nào phù hợp cho ô tiếp theo, có nghĩa là các ô trước đó đã điền sai.
      -> Lúc này hàm sẽ lui lại ô cũ, trả lại các giá trị đã điền, và thử lại với giá trị mới. Đây chính là vì sao hàm được gọi là Backtracking,

Trên trang Wikipedia về Sudoku solving algorithms có ảnh gif thể hiện các bước thử số của thuật toán quay lui này.

Sudoku Example light

Sau đây là code dựa theo video Python Sudoku Solver của Computerphile:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

def sudoku_solver(grid):
    for row in range(9):
        for col in range(9):

            # Ở đây nếu có ô vẫn chưa điền thì tiếp tujcc thử giá trị
            # Nếu đã điền hết rồi thì phương trình sẽ đi thẳng đến display_sudoku(grid)
            if grid[row][col] == 0:
                
                # Thử từng giá trị từ 1 đến 9
                for value in range(1, 10):
                    if can_input(grid, value, row, col):

                        # Nếu điền được, gọi lại hàm để giải tiếp ô tiếp theo
                        grid[row][col] = value
                        sudoku_solver(grid)

                        # Nếu hàm bên trên bị kẹt, không thể điền tiếp nữa
                        # thì ở đây sẽ trả lại về 0 và thử xét lại với giá trị khác
                        grid[row][col] = 0

                # Trả về rỗng nếu không tìm được giá trị phù hợp.
                # Lúc này hàm sẽ quay ngược lại bước điền giá trị `0`
                return
            
    # Sau khi toàn bộ bảng đã được điền thì hiện ra kết quả
    display_sudoku(grid)

Nếu không muốn sử dụng 2 vòng lặp row và col, ta cũng có thể đưa 2 giá trị này vào phần input của hàm và tăng tương ứng trong mỗi lần chạy.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

def sudoku_solver2(grid, row=0, col=0):
    if col == 9:
        if row == 8:
            # Nếu đã đến cột cuối, dòng cuối rồi thì là đã giải xong, in ra sudoku
            display_sudoku(grid)
            return
        
        # Nếu chưa đến dòng cuối, thì tăng số dòng +1, chuyển cột về 0
        sudoku_solver2(grid, row+1, 0)

    else:
        if grid[row][col] == 0:

            # Thử từng giá trị từ 1 đến 9
            for value in range(1, 10):
                if can_input(grid, value, row, col):

                    # Nếu điền được, gọi lại hàm để giải tiếp ô ở cột tiếp theo
                    grid[row][col] = value
                    sudoku_solver2(grid, row, col+1)

                    # Nếu hàm bên trên bị kẹt, không thể điền tiếp nữa
                    # thì ở đây sẽ trả lại về 0 và thử xét lại với giá trị khác
                    grid[row][col] = 0

        # Nếu ô hiện tại không trống thì qua cột tiếp theo
        else:
            sudoku_solver2(grid, row, col+1)

Cá nhân mình thấy cách 2 dễ hiểu hơn, và về thời gian xử lý cũng nhanh hơn một chút so với cách 1

1
2
3
4
5

>>> %timeit sudoku_solver(sudoku_input)
2.58 ms ± 636 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

>>> %timeit sudoku_solver2(sudoku_input)
3.27 ms ± 1.08 ms per loop (mean ± std. dev. of 7 runs, 100 loops each)

Nhưng đổi lại thì số lần gọi hàm của cách 2 sẽ nhiều hơn cách 1, bởi vì chúng ta có đoạn check row và col, rồi lại tiếp tục call hàm để nếu xuống dòng. Ở mục tiếp theo mình sẽ bàn về cách thêm bộ đếm để kiểm tra số lần hàm được gọi.

Đặc điểm và trường hợp tệ nhất của hàm quay lui

Nhìn vào ý tưởng và code, chúng ta cũng thấy được một số đặc điểm sau:

[1] Code vẫn sẽ chạy cho đến khi thử toàn bộ giá trị

Để kiểm tra việc này, chúng ta có thể thêm một hàm để đếm như sau

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

function_calls = 0            # Tạo giá trị bộ đếm

def sudoku_solver(grid):
    global function_calls     # Thêm bộ đếm vào hàm
    function_calls += 1       # +1 mỗi lần chạy function
    for row in range(9):
        for col in range(9):
            if grid[row][col] == 0:
                for value in range(1, 10):
                    if can_input(grid, value, row, col):
                        grid[row][col] = value
                        sudoku_solver(grid)
                        grid[row][col] = 0
                return
    display_sudoku(grid)

    # Hiển thị thời điểm hàm được giải
    print(f"Solved after calling sudoku_solver: {function_calls} times.")


sudoku_grid = [[0, 0, 0, 0, 0, 2, 0, 3, 0],
               [0, 0, 5, 8, 0, 0, 9, 0, 0],
               [9, 0, 0, 0, 0, 5, 0, 0, 0],
               [0, 1, 3, 4, 0, 6, 0, 8, 0],
               [0, 6, 0, 0, 0, 0, 0, 7, 0],
               [0, 8, 0, 5, 0, 1, 6, 4, 0],
               [0, 0, 0, 3, 0, 0, 0, 0, 6],
               [0, 0, 2, 0, 0, 7, 4, 0, 0],
               [0, 7, 0, 6, 0, 0, 0, 0, 0]]
sudoku_solver(sudoku_input)

# Xuất ra giá trị function_calls cuối
print(f"Total calls sudoku_solver: {function_calls} times.")

Output

1
2
3
4
5
6
7
8
9
10
11
12
13

8 4 7 | 9 6 2 | 1 3 5 
1 2 5 | 8 4 3 | 9 6 7 
9 3 6 | 7 1 5 | 8 2 4 
------+-------+------
2 1 3 | 4 7 6 | 5 8 9 
5 6 4 | 2 9 8 | 3 7 1 
7 8 9 | 5 3 1 | 6 4 2 
------+-------+------
4 5 8 | 3 2 9 | 7 1 6 
6 9 2 | 1 8 7 | 4 5 3 
3 7 1 | 6 5 4 | 2 9 8 
Solved after calling sudoku_solver: 17368 times.
Total calls sudoku_solver: 18223 times.

[2] Chúng ta thử giá trị từ 1 đến 9, vậy trường hợp xấu nhất đó là các giá trị trong 1 hàng có thứ tự 9,8,7,6,5,4,3,2,1

Chúng ta sẽ thử với sudoku_grid2

1
2
3
4
5
6
7
8
9

sudoku_grid2 = [[0, 0, 0, 0, 0, 0, 0, 0, 0],
                [0, 0, 0, 0, 0, 3, 0, 8, 5],
                [0, 0, 1, 0, 2, 0, 0, 0, 0],
                [0, 0, 0, 5, 0, 7, 0, 0, 0],
                [0, 0, 4, 0, 0, 0, 1, 0, 0],
                [0, 9, 0, 0, 0, 0, 0, 0, 0],
                [5, 0, 0, 0, 0, 0, 0, 7, 3],
                [0, 0, 2, 0, 1, 0, 0, 0, 0],
                [0, 0, 0, 0, 4, 0, 0, 0, 9]]

Lúc này hàm sudoku_solver sẽ mất rất lâu để tìm ra kết quả. Nhưng nếu chúng ta sửa lại cách check số từ 9 đến 1, thì ta sẽ có được kết quả ngay lập tức (mặc dù hàm vẫn chạy, vì tính chất [1])

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

def sudoku_solver_reversed(grid):
    for row in range(9):
        for col in range(9):
            if grid[row][col] == 0:

                # Đổi range(1, 10) thành chiều ngược lại
                for value in range(9,0,-1):
                    if can_input(grid, value, row, col):
                        grid[row][col] = value
                        sudoku_solver(grid)
                        grid[row][col] = 0
                return
    display_sudoku(grid)

sudoku_solver_reversed(sudoku_grid2)

Output

1
2
3
4
5
6
7
8
9
10
11

9 8 7 | 6 5 4 | 3 2 1 
2 4 6 | 1 7 3 | 9 8 5 
3 5 1 | 9 2 8 | 7 4 6 
------+-------+------
1 2 8 | 5 3 7 | 6 9 4 
6 3 4 | 8 9 2 | 1 5 7 
7 9 5 | 4 6 1 | 8 3 2 
------+-------+------
5 1 9 | 2 8 6 | 4 7 3 
4 7 2 | 3 1 9 | 5 6 8 
8 6 3 | 7 4 5 | 2 1 9

Thêm cơ chế dừng cho hàm backtracking

Ừ thì mình đã có được lời giải cho hàm sudoku_solver_reversed rồi đấy. Nhưng hàm vẫn cứ chạy hoài, vậy có cách nào để dừng sau khi tìm được kết quả không? Một cách mình thử áp dụng đó là cho hàm trả về good khi đã giải xong.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

def sudoku_solver_reversed(grid):
    for row in range(9):
        for col in range(9):
            if grid[row][col] == 0:
                for value in range(9,0,-1):
                    if can_input(grid, value, row, col):
                        grid[row][col] = value

                        # Nếu trong các bước tiếp theo trả về "good"
                        # thì trả về "good" để ngừng vòng lặp này
                        if sudoku_solver(grid) == "good":
                            return "good"
                        grid[row][col] = 0

                # Trong trường hợp thử hết giá trị mà không điền được
                # Trả về "bad" để thông báo rằng các giá trị trước cần chuyển về 0
                return "bad"
    display_sudoku(grid)

    # Trả về "good" sau khi đã giải xong
    return "good"

Các nguồn tham khảo và mở rộng

Hình ảnh được tạo bằng công cụ Figma

Algorithm, Sudoku
algorithm recursion sudoku backtracking
Bài viết này được cấp phép bởi tác giả theo giấy phép CC BY 4.0 .