Bài viết

Về hồi quy tuyến tính đơn biến và Phương pháp Hạ Gradient

Đăng lúc Cập nhật lúc
11 phút đọc

Trong bài này mình sẽ bàn về phương trình hồi quy tuyến tính của 1 biến trong mô hình học máy, và phương pháp hạ gradient trong mô hình này.

Xác định mục tiêu

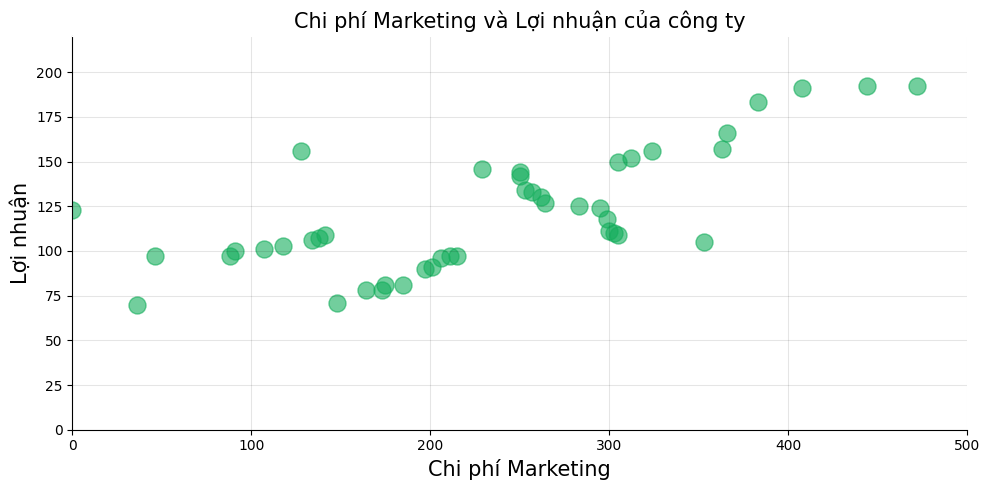
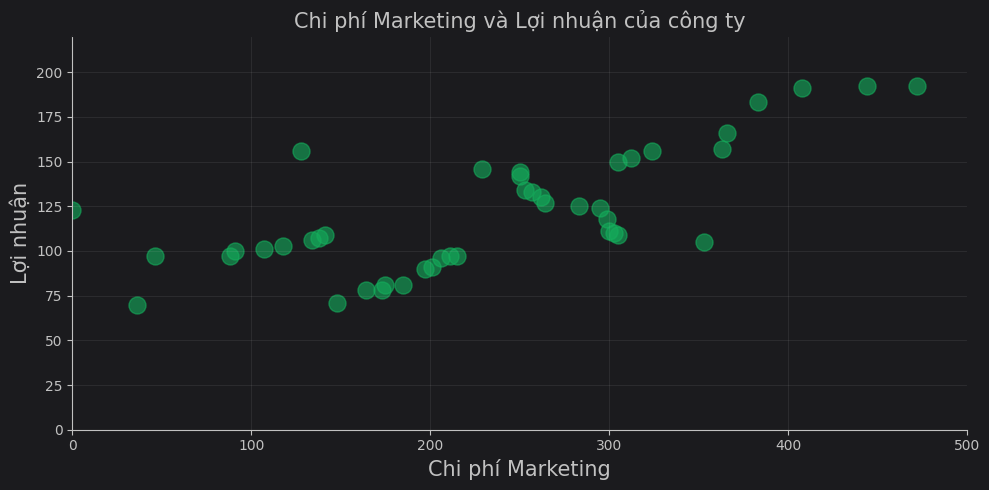
Giả sử chúng ta có một bảng thống kê các lần chi tiêu cho bộ phận Marketing (cột Marketing) và lợi nhuận thu về từ các lần vận hành (cột Profit):

MarketingProfit
472192
444192
408191
383183
……
16478
14871
3670

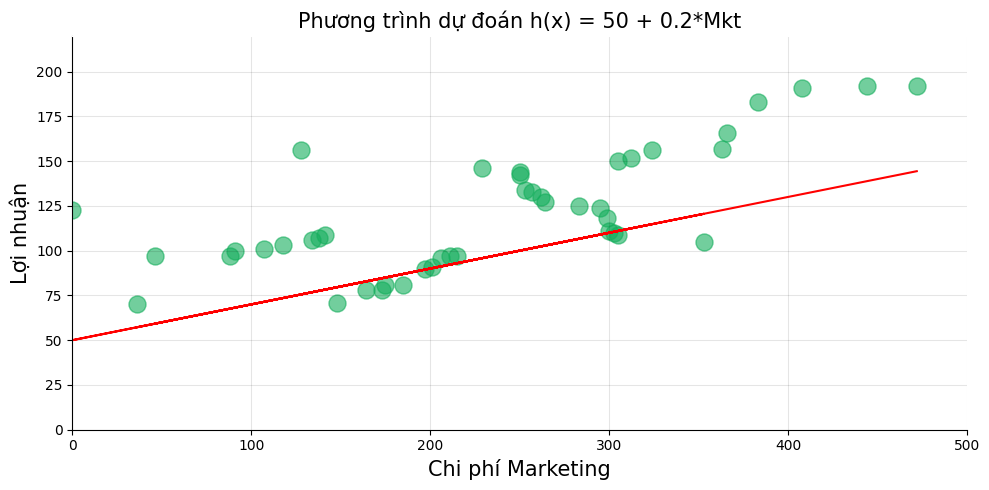
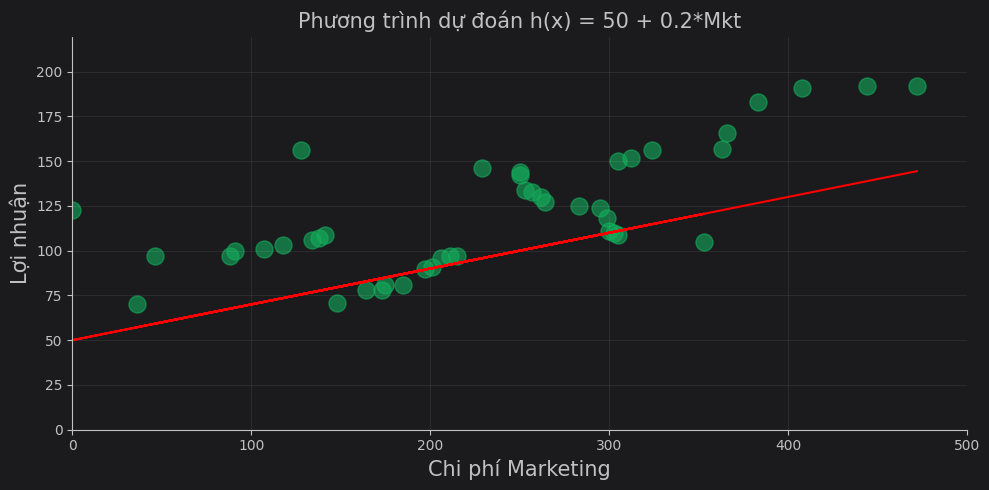
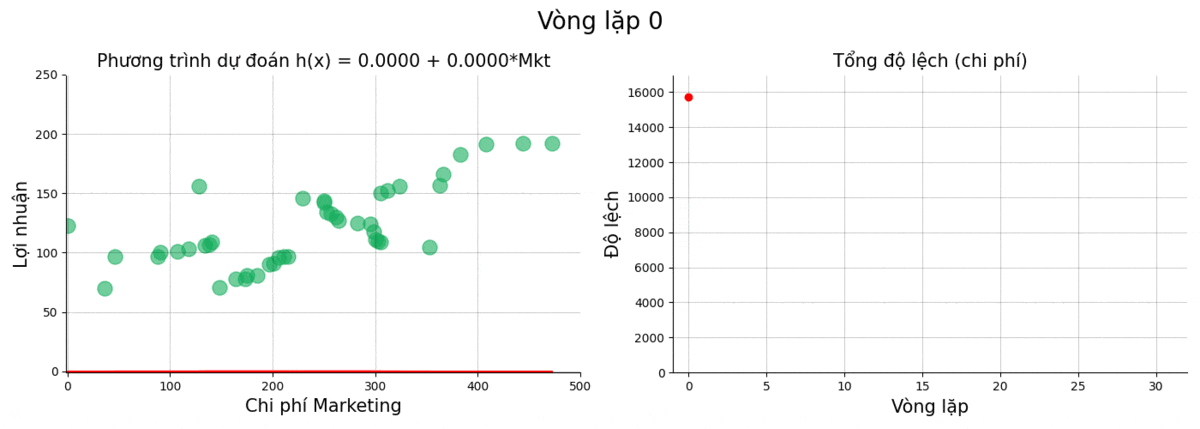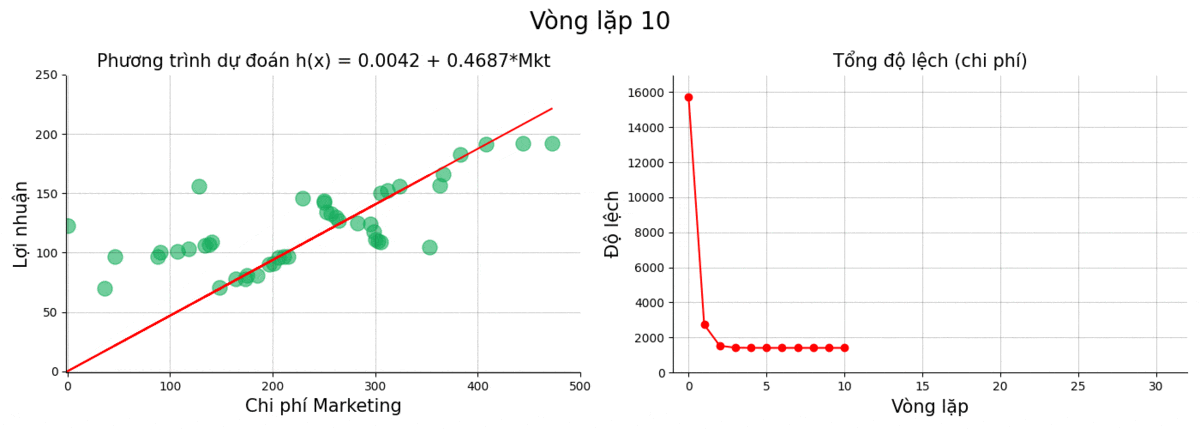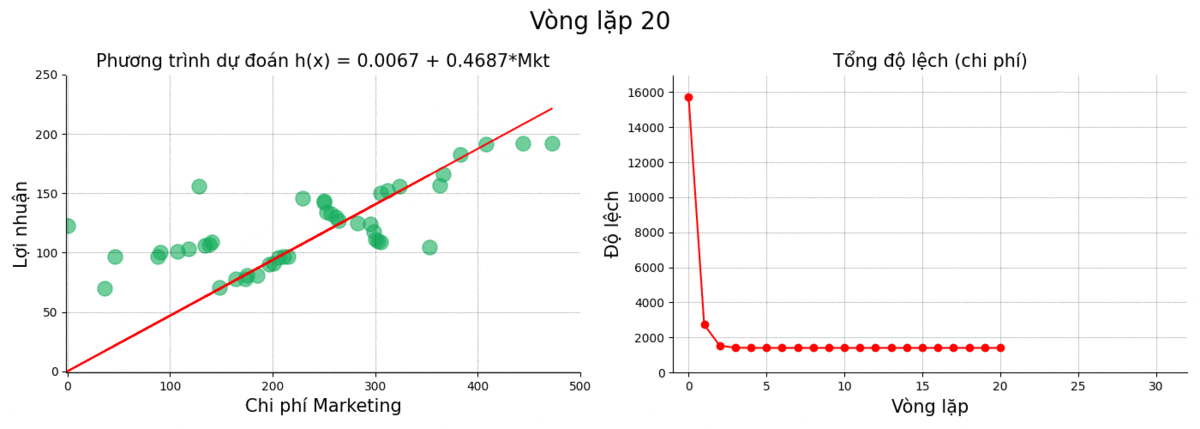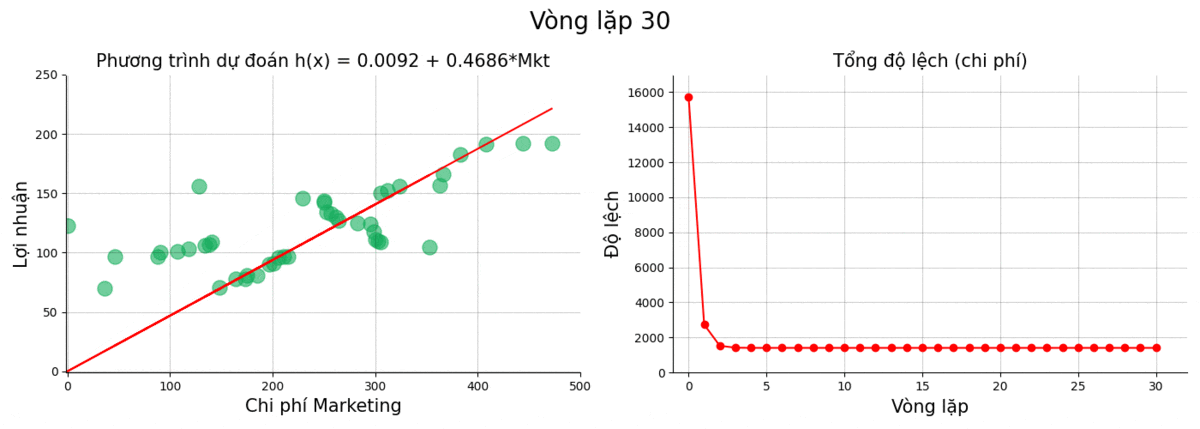
Biểu diễn bằng biểu đồ phân tán (scatter plot chart)

Marketing vs Profit chart light Marketing vs Profit chart dark

Mục tiêu của chúng ta là cần tìm một phương trình đường thẳng, mà ở đó ta có thể biểu diễn được mối quan hệ giữa chi phí cho Marketing và lợi nhuận Profit thu về. Phương trình cần tìm của chúng ta có dạng như sau:

\[h(x) = \text{Profit} = w_0 + w_1 \times \text{Marketing}\]

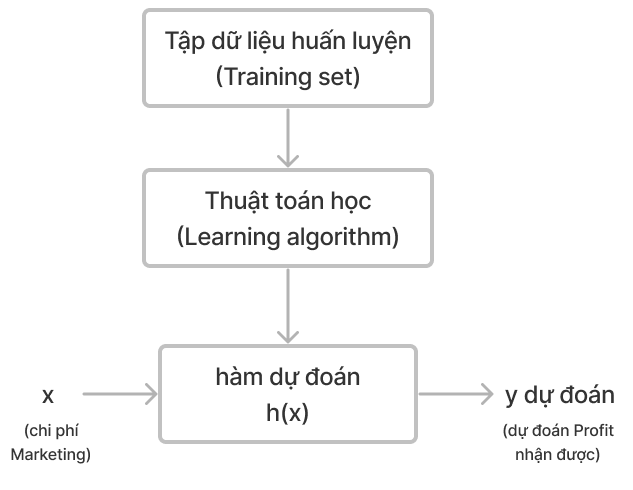
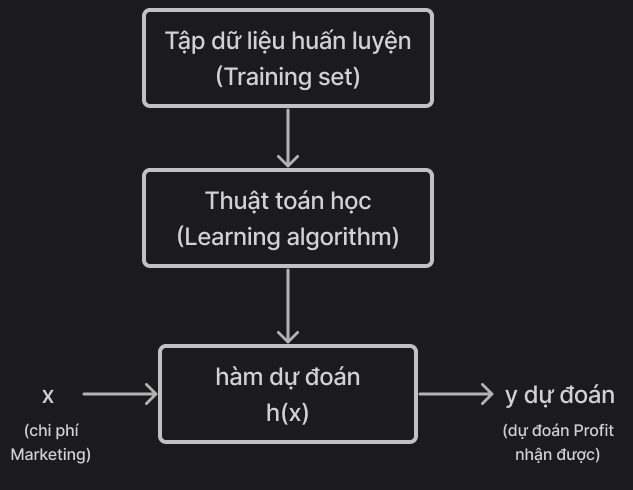
Chúng ta có flow xử lý bài toán như sau:

Linear Regression process light Linear Regression process dark

Sai số giữa giá trị dự đoán và thực tế

Giả định chúng ta đoán mò phương trình $h(x)$ với $w_0 = 50$ và $w_1 = 0.2$:

\[\text{Profit dự đoán} = h(x) = 50 + 0.2 \times \text{Marketing}\]

Chúng ta có giá trị dự đoán như sau

MarketingProfith(x) =
50 + 0.2*Mkt
472192161.6
444192153.2
408191142.4
………
1647869.2
1487164.4
367030.8

Sample prediction line light Sample prediction line dark

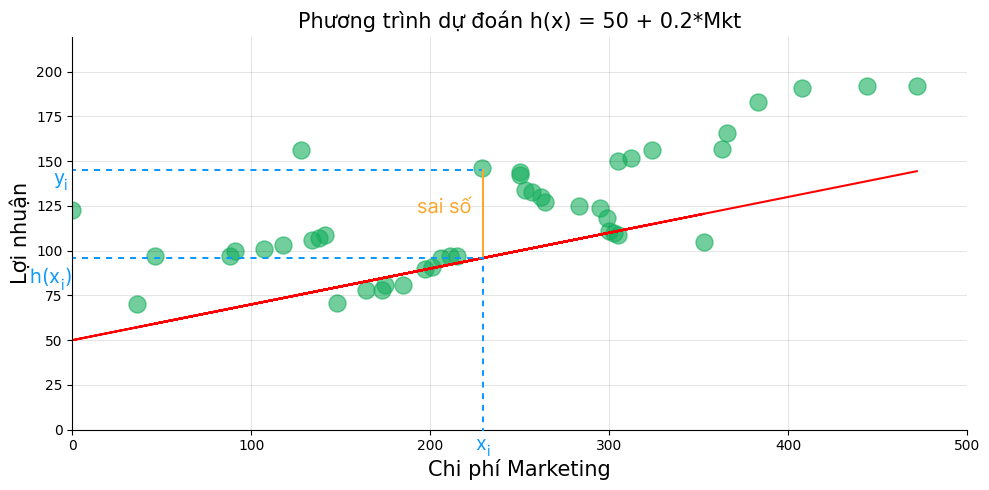
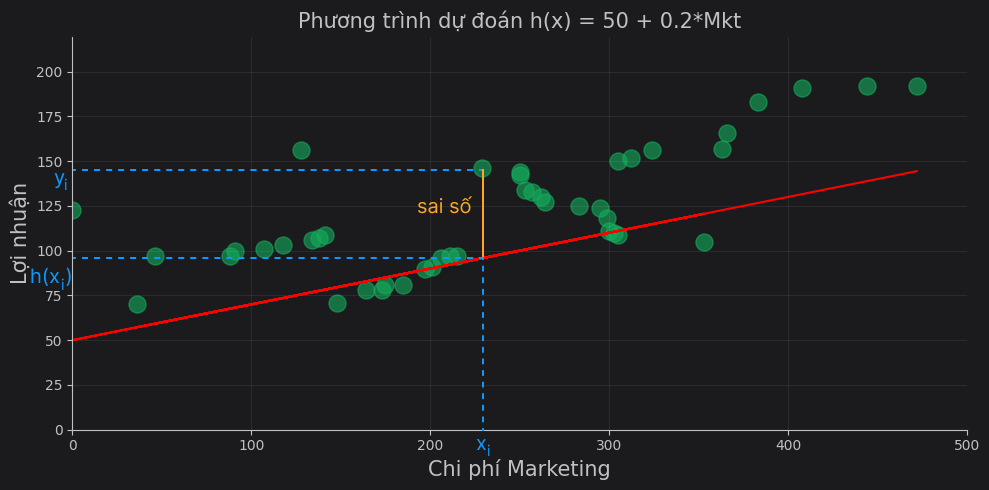
Chúng ta có thể tính được sai số (độ chênh lệch) giữa giá trị dự đoán $h(x)$ và giá trị thực tế Profit. Ta thiết lập phương trình tính sai số tại giá trị ngẫu nhiên $x_i$ như sau:

\[\begin{align} \text{sai số tại $x_i$} &= |\text{Profit tại $x_i$} - \text{Dự đoán tại $x_i$}| \\ &= |y_i - h(x_i)| \end{align}\]

Distance between real value vs predict light Distance between real value vs predict dark

Lưu ý, đối với hàm dự đoán cho phương trình hồi quy một biến, các cách viết sau đều như nhau:
$\hat{y} = h_\theta(x) = h(x) = \theta_0 + \theta_1x = w_0 + w_1x $

Hàm mất mát và Hàm chi phí

Trước tiên, chúng ta cùng nhắc lại phương trình sai số toàn phương trung bình (Mean Square Error):

\[\begin{align} \text{MSE} &= \frac{1}{n} [(y_1 - \hat{y}_1)^2 + (y_2 - \hat{y}_2)^2 + \dots + (y_n - \hat{y}_n)^2] \\ &= \frac{1}{n} \sum_{j=1}^n (y_j - \hat{y_j})^2 \end{align}\]

Ở đây, chúng ta dùng chính phương trình MSE làm hàm chi phí của bài toán. Với:

  • Hàm mất mát (loss function) là bình phương độ lệch của giá trị dự đoán $\hat{y}_i = h(x_i)$ so với giá trị $y_i$ tại điểm $x_i$:
\[l^{(i)}(w_0, w_1) = (y_i - \hat{y_i})^2\]
  • Hàm chi phí (cost function) là hàm khái quát của hàm mất mát, thể hiện trung bình độ lệch của toàn mẫu trong tập huấn luyện $\rightarrow$ chi phí tính toán:
\[\begin{align} L(w_0, w_1) &= \frac{1}{n} \Big[ (y_1 - \hat{y}_1)^2 + \dots + (y_n - \hat{y}_n)^2 \Big] \\[1ex] &= \frac{1}{n} \sum_{j=1}^{n} (y_j - \hat{y}_j)^2 \end{align}\]

Để mô hình dự đoán được chính xác nhất, ta cần phải khiến cho giá trị của hàm mất mát là nhỏ nhất.

Hạ độ dốc (thường gọi là Hạ Gradient - Gradient descent)

Bây giờ, mục tiêu của chúng ta là tìm cặp giá trị $w_0$ và $w_1$ sao cho hàm chi phí đạt giá trị nhỏ nhất, nhưng chúng ta vẫn chưa thấy $w_0$ và $w_1$ trong hàm Cost function. Ta viết lại như sau:

Với $\hat{y_j} = h(x_j) = w_0 + w_1x$

\[\begin{align} L(w_0, w_1) &= \frac{1}{n} \sum_{j=1}^{n} (y_j - \hat{y}_j)^2 \\ &= \frac{1}{n} \sum_{j=1}^{n} \big[y_j - (w_0 + w_1x_j) \big]^2 \end{align}\]

Phương pháp hạ gradient giúp chúng ta xác định được đâu là hướng mà $w_0$ và $w_1$ nên tăng/giảm để hàm mất mát đạt giá trị cực tiểu. Chúng ta sẽ dùng phương pháp đạo hàm để xác định giá trị cực tiểu của hàm số. Và vì phương trình có 2 biến $w_0$ và $w_1$, ta sẽ dùng cụ thể phương pháp đạo hàm riêng.

Đạo hàm với $w_0$

\[\begin{align} \frac{\partial}{\partial w_0} L(w_0, w_1) &= \frac{\partial}{\partial w_0} \Bigg[\frac{1}{n} \sum_{j=1}^{n} [y_j - (w_0 + w_1x_j)]^2 \Bigg] \\[2ex] &= \frac{1}{n} \sum_{j=1}^{n} \frac{\partial}{\partial w_0} \bigg[ [y_j - (w_0 + w_1x_j)]^2 \bigg] \\[2ex] &= \frac{1}{n} \sum_{j=1}^{n} 2[y_j - (w_0 + w_1x_j)] (-1) \\ &= \frac{2}{n} \sum_{j=1}^{n} (w_0 + w_1x_j - y_j) \\ \end{align}\]

Đạo hàm với $w_1$

\[\begin{align} \frac{\partial}{\partial w_1} L(w_0, w_1) &= \frac{\partial}{\partial w_1} \Bigg[\frac{1}{n} \sum_{j=1}^{n} [y_j - (w_0 + w_1x_j)]^2 \Bigg] \\[2ex] &= \frac{1}{n} \sum_{j=1}^{n} \frac{\partial}{\partial w_1} \bigg[ [y_j - (w_0 + w_1x_j)]^2 \bigg] \\[2ex] &= \frac{1}{n} \sum_{j=1}^{n} 2 \big[y_j - (w_0 + w_1x_j) \big] (- x_j) \\ &= \frac{2}{n} \sum_{j=1}^{n} x(w_0 + w_1x_j - y_j) \\ \end{align}\]

Cập nhật tham số $w_0$ và $w_1$ và xác định đường thẳng hồi quy tuyến tính

Để hàm đi đến giá trị cực tiểu, chúng ta cần:

  • Cập nhật giá trị $w_0$ và $w_1$ theo phương hướng của đạo hàm
  • Đi từng bước nhỏ để tránh vượt lố giá trị (và có khả năng không bao giờ đến được giá trị cực tiểu) $\rightarrow$ tạo giá trị learning_rate $\alpha$

Update đồng thời trong vòng lặp:

\[\begin{align} w_0 &:= w_0 - \alpha \frac{2}{n} \sum_{j=1}^{n} (w_0 + w_1x_j - y_j) \\ w_1 &:= w_1 - \alpha \frac{2}{n} \sum_{j=1}^{n} x(w_0 + w_1x_j - y_j) \end{align}\]

Lưu ý rằng ở đây cần update $w_0$ và $w_1$ đồng thời (hoặc sử dụng biến tạm) để tránh bị sai lệch giá trị.

Để hiểu rõ hơn về chuyện gì sẽ xảy ra khi ta cập nhật giá trị trong trong Gradient descent, chúng ta có thể tham khảo video giải thích sau đây của thầy Andrew Ng.

Như vậy là chúng ta đã xong ý tưởng để xây dựng thuật toán Hồi quy tuyến tính đơn biến. Bây giờ chúng ta có thể bắt tay vào viết code.

Xây dựng code

Ở đây, chúng ta sẽ xây dựng hàm với ví dụ được đưa ra.

\[\text{Profit}_\text{dự đoán} = \hat{y} = h(x) = w_0 + w_1* \text{Marketing}\]

Hàm chi phí

\[\begin{align} L(w_0, w_1) &= \frac{1}{n} \sum_{j=1}^{n} (y_j - \hat{y}_j)^2 \\ &= \frac{1}{n} \sum_{j=1}^{n} \big[y_j - (w_0 + w_1x_j) \big]^2 \end{align}\]
1
2
3
4
5
6
7
8

def cost_function(marketing, profit, w0, w1):
    data_size = len(marketing)
    total_error = 0

    for i in range(data_size):
        total_error += (profit[i] - (w0 + w1*marketing[i]))**2

    return total_error / data_size

Tính tham số bằng phương pháp hạ độ dốc

\[\begin{align} w_0 &:= w_0 - \alpha \frac{2}{n} \sum_{j=1}^{n} (w_0 + w_1x_j - y_j) \\ w_1 &:= w_1 - \alpha \frac{2}{n} \sum_{j=1}^{n} x(w_0 + w_1x_j - y_j) \end{align}\]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

def gradient_descent(marketing, profit, w0_input, w1_input, learning_rate):
    w0_gradient = 0
    w1_gradient = 0
    data_size = len(marketing)

    # Tính tổng đạo hàm
    for i in range(data_size):
        # Đạo hàm w0
        w0_gradient += (w0_input + w1_input*marketing[i] - profit[i])

        # Đạo hàm w1
        w1_gradient += marketing[i]*(w0_input + w1_input*marketing[i] - profit[i])

    # Cập nhật giá trị tham số
    w0_new = w0_input - 2 * learning_rate * w0_gradient / data_size
    w1_new = w1_input - 2 * learning_rate * w1_gradient / data_size
    
    return w0_new, w1_new

Hàm huấn luyện mô hình

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

def train(marketing, profit, w0, w1, learning_rate, loop_count):
    # Tính cost và in ra giá trị đầu vào
    cost = cost_function(marketing, profit, w0, w1)
    print(f"loop=0    w0={w0:.4f}    w1={w1:.4f}    cost={cost:.4f}")
    
    # Lưu giá trị đầu vào
    w0_records = [w0]
    w1_records = [w1]
    cost_records = [cost]

    for loop in range(1, loop_count+1):
        # Cập nhật tham số
        w0, w1 = gradient_descent(marketing, profit, w0, w1, learning_rate)
        w0_records.append(w0)
        w1_records.append(w1)

        # Tính chi phí (độ sai lệch)
        cost = cost_function(marketing, profit, w0, w1)
        cost_records.append(cost)

        # In ra giá trị tại một số vòng lặp
        if (loop < 6) or (loop % 10 == 0):
            print(f"loop={loop}    w0={w0:.4f}    w1={w1:.4f}    cost={cost:.4f}")

    return w0_records, w1_records, cost_records

Chạy chương trình với biến đầu vào

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# Load thư viện
import pandas as pd
import matplotlib.pyplot as plt

# Load dữ liệu
df = pd.read_csv("sample_data.csv")

# Chạy mô hình, lưu lại giá trị w0, w1 cuối và cost record của từng bước huấn luyện
w0, w1, cost_record = train(
    marketing = df['Marketing'].values, 
    profit = df['Profit'].values, 
    w0 = 0, 
    w1 = 0, 
    learning_rate = 0.00001, 
    loop_count = 30
)

Kết quả

Sau đây là kết quả của quá trình train tại một số điểm chọn lọc

loop$w_0$$w_1$cost
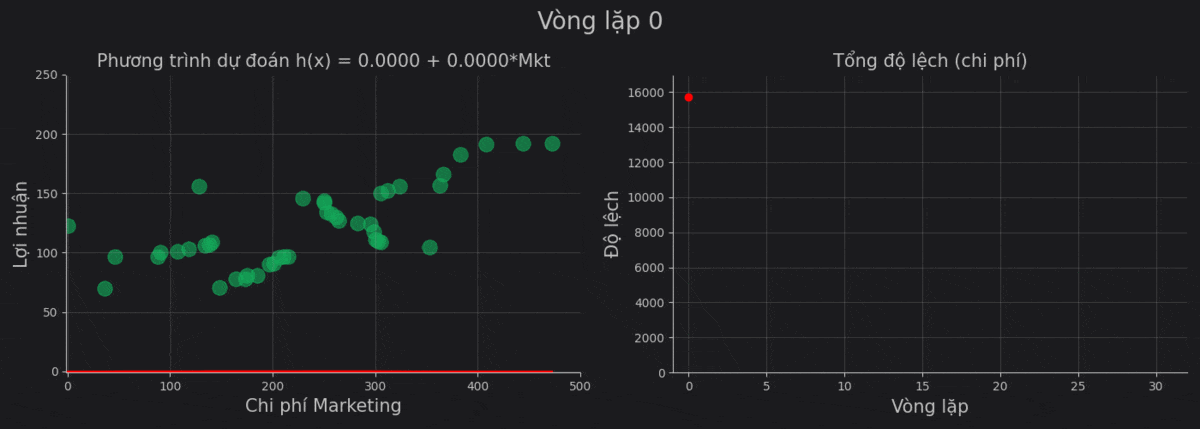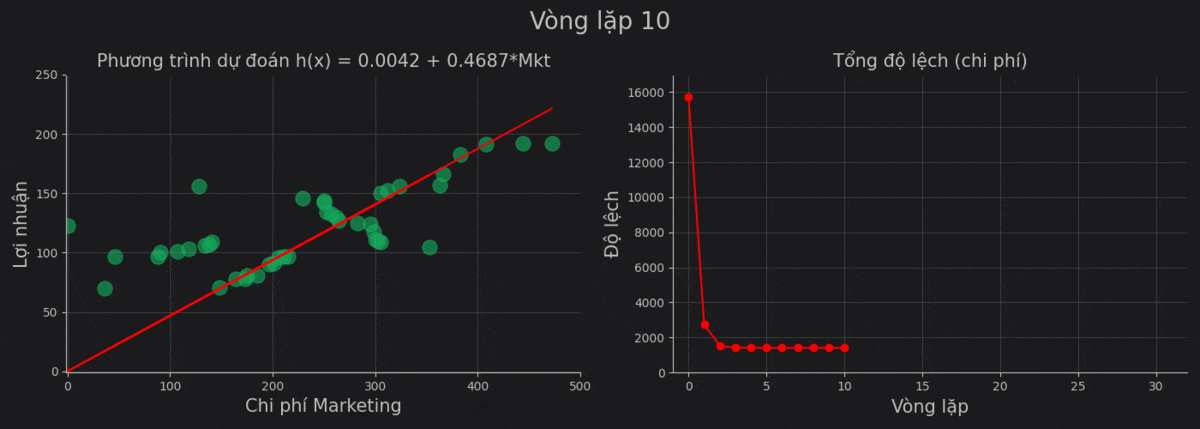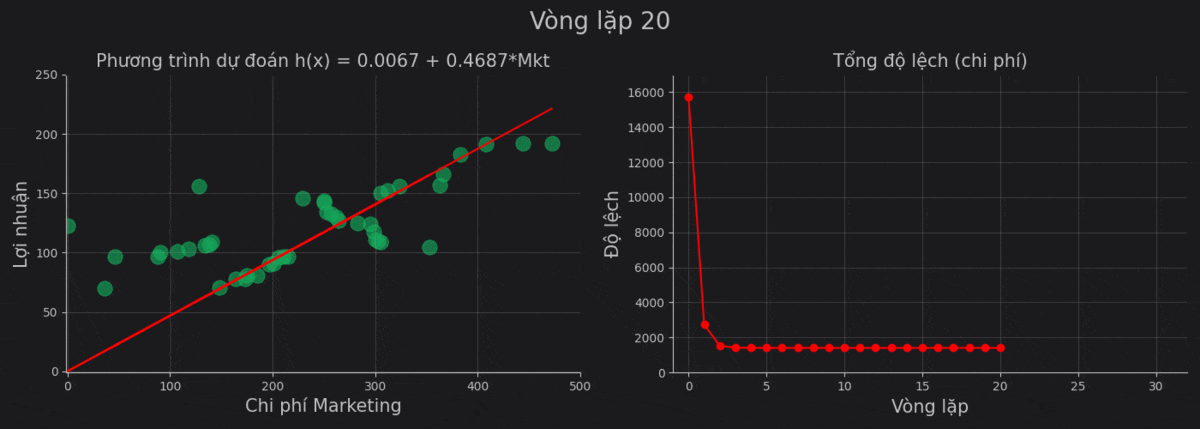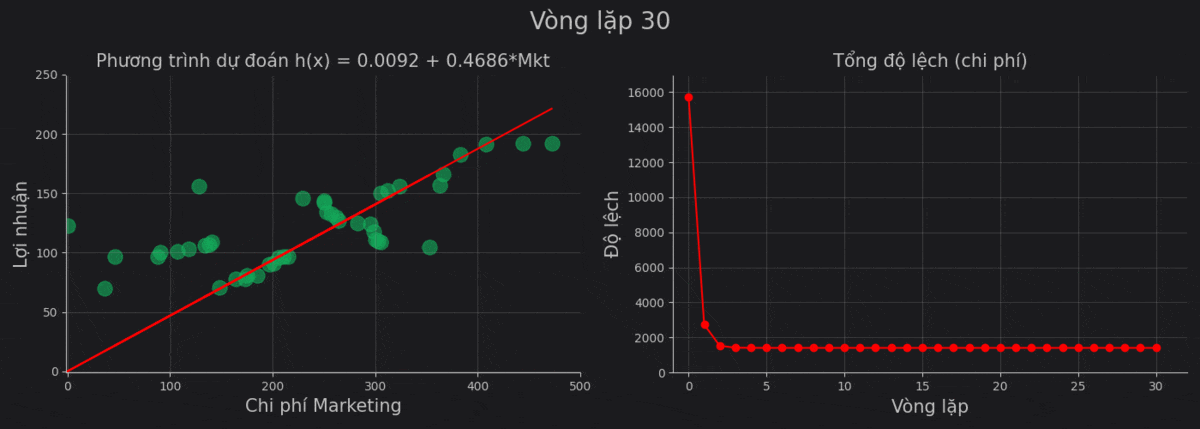
00015733.8636
10.00240.61142735.1620
20.00200.42521529.4739
30.00250.48191417.6357
40.00270.46461407.2565
50.00290.46991406.2880
100.00420.46871406.1579
200.00670.46871406.0945
300.00920.46861406.0312

Sử dụng giá trị cuối, ta thu được phương trình:

\[h(x) = \text{Profit} = 0.0092 + 0.4686 \times \text{Marketing}\]

Cùng nhìn lại quá trình vòng lặp hạ gradient.

Linear Regression result light Linear Regression result dark

Chúng ta thấy rằng từ vòng lặp thứ 4 trở về sau thì kết quả gần như thay đổi rất ít. Điều này có thể là do: giá trị đạo hàm của cost function thấp, learning_rate thấp, hoặc do kết quả của chúng ta đang ở một trong những vùng đáy cực tiểu.

Nhận xét về giá trị của tốc độ học (Learning Rate)

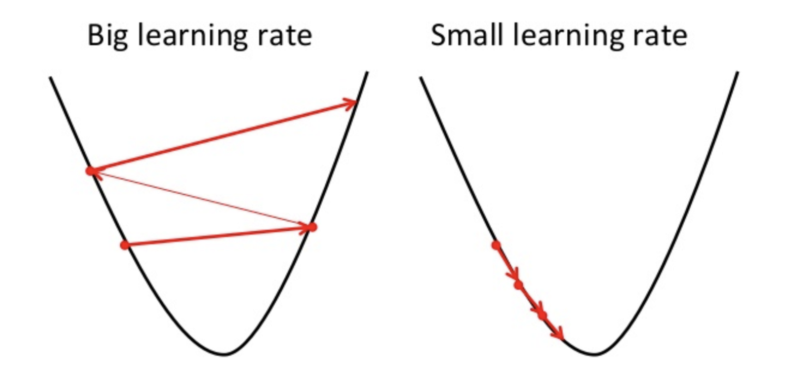
Learning Rate on the result of Gradient Descent

Khi tốc độ học quá cao

Khi giá trị của tốc độ học quá cao, $w_0$ và $w_1$ mới cho ra kết quả lệch nhiều so với vị trí cực tiểu mà ta mong muốn.

Chúng ta có thể thử chạy mô hình với các giá trị sau đây

1
2
3
4
5
6
7
8
9

# Chạy huấn luyện mô hình
w0_records, w1_records, cost_record = train(
    marketing = df['Marketing'].values, 
    profit = df['Profit'].values, 
    w0 = 50, 
    w1 = 0.2, 
    learning_rate = 0.0001, 
    loop_count = 30
)

Sau đây là kết quả nhận được

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

| loop |        w_0       |        w_1         |        cost       |
|------|------------------|--------------------|-------------------|
|    0 |           50.000 |              0.200 |         1 138.442 |
|    1 |           50.005 |              1.391 |        79 466.038 |
|    2 |           49.955 |           - 12.954 |    11 444 440.523 |
|    3 |           50.569 |            159.840 | 1 660 449 935.317 |
|    4 |           43.185 |        - 1 921.564 |      2.41 * 10^11 |
|    5 |          132.134 |         23 150.102 |      3.50 * 10^13 |
|    6 |         -939.297 |      - 278 852.024 |      5.07 * 10^15 |
|    7 |       11 966.694 |      3 358 931.217 |      7.36 * 10^17 |
|    8 |    - 143 493.119 |   - 40 460 187.270 |      1.07 * 10^20 |
|    9 |    1 729 106.635 |    487 365 419.200 |      1.55 * 10^22 |
|   10 | - 20 827 396.880 | -5 870 587 010.099 |      2.25 * 10^24 |
|   20 |   - 1.34 * 10^18 |     - 3.78 * 10^20 |      9.30 * 10^45 |
|   30 |   - 8.61 * 10^28 |     - 2.43 * 10^31 |      3.84 * 10^67 |

Ta thấy rằng, giá trị cost function của chúng ta không giảm, mà còn ngày càng tăng dần theo cấp số nhân. Ta nhận xét rằng kết quả đang bị vượt quá giá trị học tối ưu (overshoot) và ngày càng ra xa khỏi giá trị thấp nhất (diverge)

Khi tốc độ học quá thấp

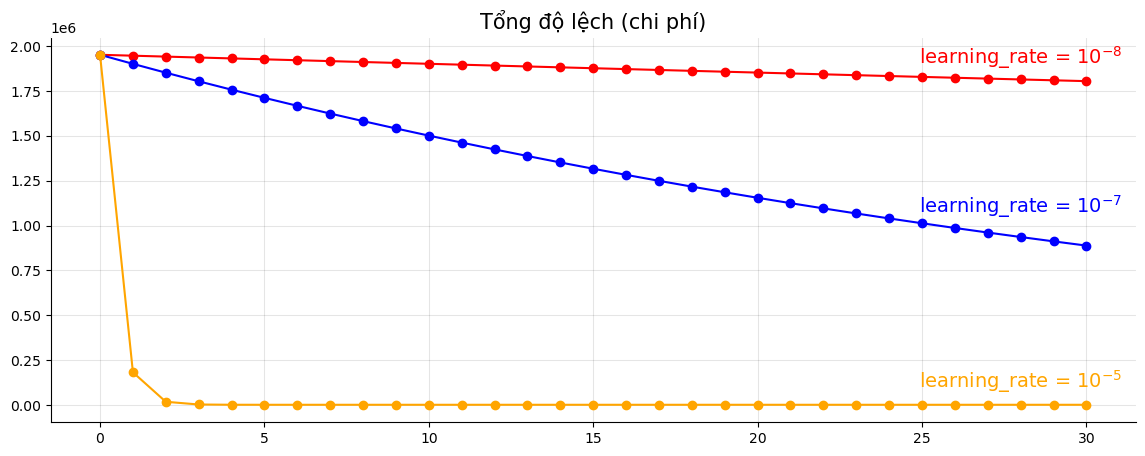
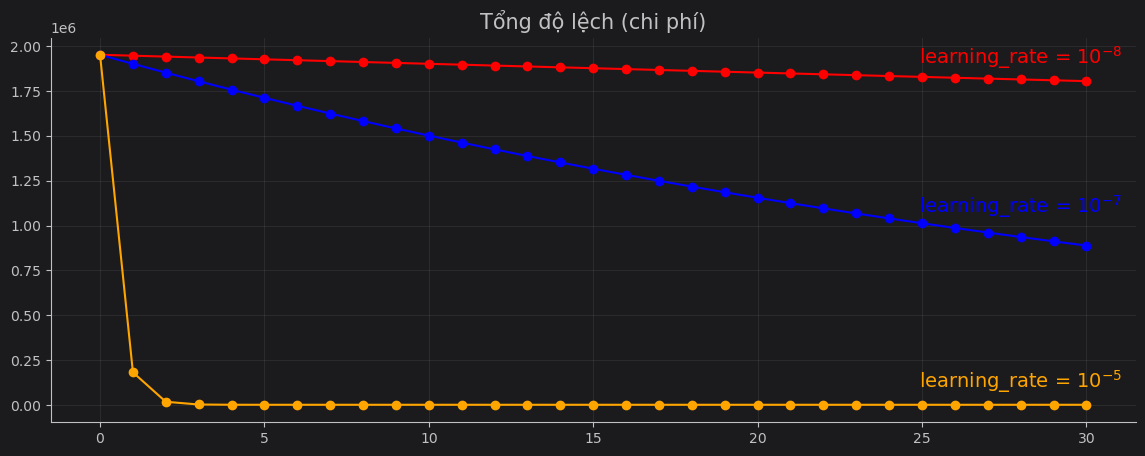
Khi giá trị của tốc độ học quá thấp, mô hình sẽ tốn rất nhiều thời gian để đi đến giá trị tối ưu, chúng ta có thể thử áp dụng với các learning rate khác nhau để xem sự khác biệt.

Ví dụ minh hoạ cho việc áp dụng tốc độ học khác nhau cho mô hình học máy với đầu vào w0 = 0, w1 = 0

Linear Regression result light Linear Regression result dark

Xin hãy tham khảo bài giảng sau của thầy Andrew Ng về Learning Rate (đoạn 5:40 đến 7:50)

Các nguồn tham khảo và mở rộng

Machine Learning, Linear Regression
machine learning linear regression gradient descent
Bài viết này được cấp phép bởi tác giả theo giấy phép CC BY 4.0 .