Về dãy số Fibonacci
Bài viết này sẽ trình bày về dãy số Fibonacci và các thuật toán trong Python để tìm số ở vị trí cho trước. Mình cũng sẽ thảo luận về hiệu suất và khả năng xử lý của các thuật toán này.
Giới thiệu
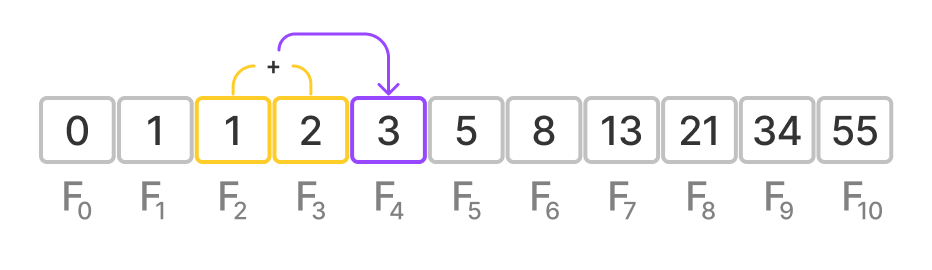
Dãy số Fibonacci là một dãy số quen thuộc bắt đầu bằng chuỗi:
\[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 \dots\]Số thứ $n$ trong dãy số Fibonacci được kí hiệu là $F_n$ hoặc $F(n)$, ta có $F_0 = 0$ và $F_1 = 1$, và với $n > 1$:
\[F_n = F_{n-1} + F_{n-2}\]Ví dụ với n = 4:
$ F_4 = F_3 + F_2 = 2 + 1 = 3 $
Tìm số Fibonacci tại vị trí n
Sử dụng vòng lặp
Ý tưởng
Ta có thể tạo một phương trình vòng lặp đơn giản với ý tưởng như sau:
- Bước 1: Bắt đầu với
a = 0vàb = 1- Lúc này a là $F_0$, b là $F_1$
- Bước 2: Cập nhật giá trị a thành $F_1$ và b thành giá trị tiếp theo $F_2 = F_1 + F_0$
- Bước 3: Tiếp tục lặp lại bước 2 đến khi a là giá trị $F_n$ cần tìm
- Bước 4: Trả về a
Thuật toán
1
2
3
4
5
def fibonacci_linear_loop(n: int) -> int:
a, b = 0, 1
for loop in range(n):
a, b = b, a + b
return a
Sử dụng công thức Binet
Giới thiệu
công thức Binet tính giá trị của $F_n$ như sau:
\[F_n = \frac{1}{\sqrt{5}}\Bigg(\bigg(\frac{1 + \sqrt{5}}{2}\bigg)^{n} - \bigg(\frac{1 - \sqrt{5}}{2}\bigg)^{n}\Bigg)\]Đặt tỉ lệ vàng $\varphi = \dfrac{1 + \sqrt{5}}{2}$
Ta cũng có thể biến đổi $\dfrac{1 - \sqrt{5}}{2} = 1 - \varphi = -\dfrac{1}{\varphi} = -\varphi^{-1} $
Ta có thể viết rút gọn thành:
\[F_n = \frac{\varphi^{n} - (-\varphi)^{-n} }{\sqrt{5}} = \frac{\varphi^n - (-\varphi)^{-n}}{2\varphi - 1}\]Thuật toán
1
2
3
4
def fibonacci_binet_formula(n: int) -> int:
phi = (1 + 5**(1/2))/2 # phi là ký hiệu của tỉ lệ vàng
fibo_n = ( phi**n - (-phi)**(-n) )/(2*phi - 1)
return int(fibo_n)
Rút gọn
Ta nhận xét rằng giá trị $ \Bigg| \bigg(\dfrac{1 - \sqrt{5}}{2} \bigg)^{\displaystyle n} \Bigg| < 1 $, và giá trị này tiến rất nhanh về $0$ khi $n$ tăng. Vì thế, ta có thể tính vắn tắt giá trị $F_n$ theo:
\[F_n = \Bigg[ \frac{ \big(\frac{1 +\sqrt{5}}{2}\big)^{n}} {\sqrt{5}} \Bigg] = \Bigg[ \frac{\varphi^{n}}{2\varphi - 1} \Bigg]\]Với ngoặc vuông [ ] là phép làm tròn đến giá trị nguyên gần nhất.
Đoạn mã python cho phương trình vắn tắt
1
2
3
4
5
6
7
8
9
10
def fibonacci_binet_formula_short(n: int) -> int:
sqrt5 = 5**(1/2)
fibo_n = ((1 + sqrt5)/2)**n / sqrt5
return int(round(fibo_n))
# Hoặc
def fibonacci_binet_formula_short(n: int) -> int:
phi = (1 + 5**(1/2))/2 # phi là ký hiệu của tỉ lệ vàng
fibo_n = (phi**n)/(2*phi - 1)
return int(round(fibo_n))
Tuy nhiên, công thức Binet cần tính toán với số thập phân, và Python có một số hạn chế trong việc lưu trữ giá trị thập phân dẫn đến khả năng sai số khi tính các số Fibonacci lớn. Vì vậy trong thực tế sẽ ít được sử dụng.
Sử dụng hàm đệ quy
Ý tưởng
Hàm đệ quy đi tìm $F_n$ bằng cách truy ngược về giá trị ban đầu là $F_1$ và $F_0$, ta có:
\[\begin{aligned} F_n &= F_{n-1} + F_{n-2} \\ F_{n-1} &= F_{n-2} + F_{n-3} \\ F_{n-2} &= F_{n-3} + F_{n-4} \\ &\dots \\ F_3 &= F_2 + F_1 \\ F_2 &= F_1 + F_0 \\ \end{aligned}\]Thay $F_1 = 1$ và $F_0 = 0$, như vậy từ đấy ta tính ngược lên các giá trị $F_3, F_4, \dots$, ta tìm được giá trị $F_n$
Thuật toán
Code python khi triển khai rất gọn
1
2
3
4
def fibonacci_recursive(n: int) -> int:
if n <= 1:
return n # fib(0) = 0 và fib(1) = 1
return fibonacci_recursive(n-1) + fibonacci_recursive(n-2)
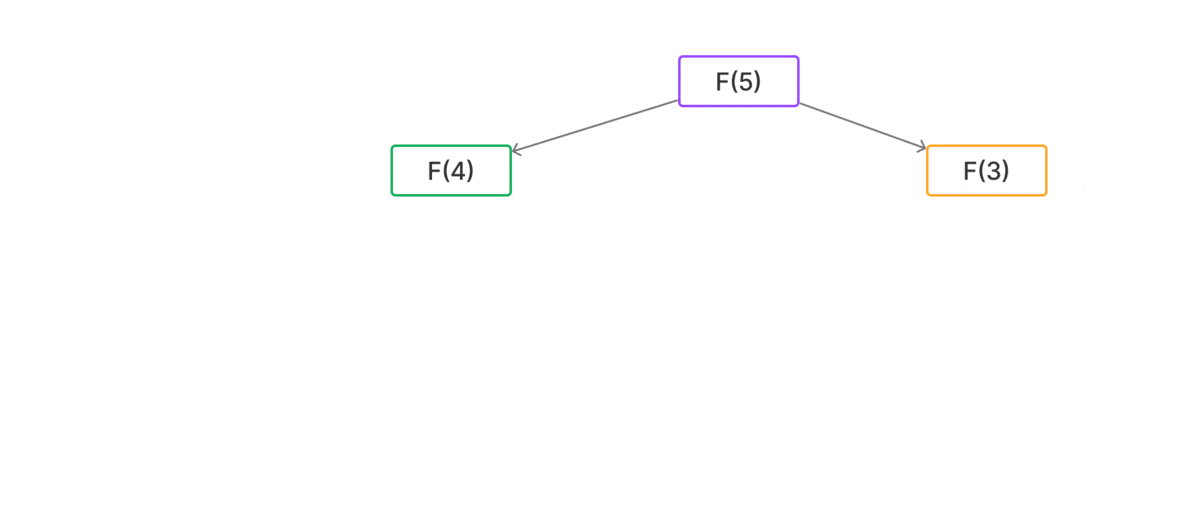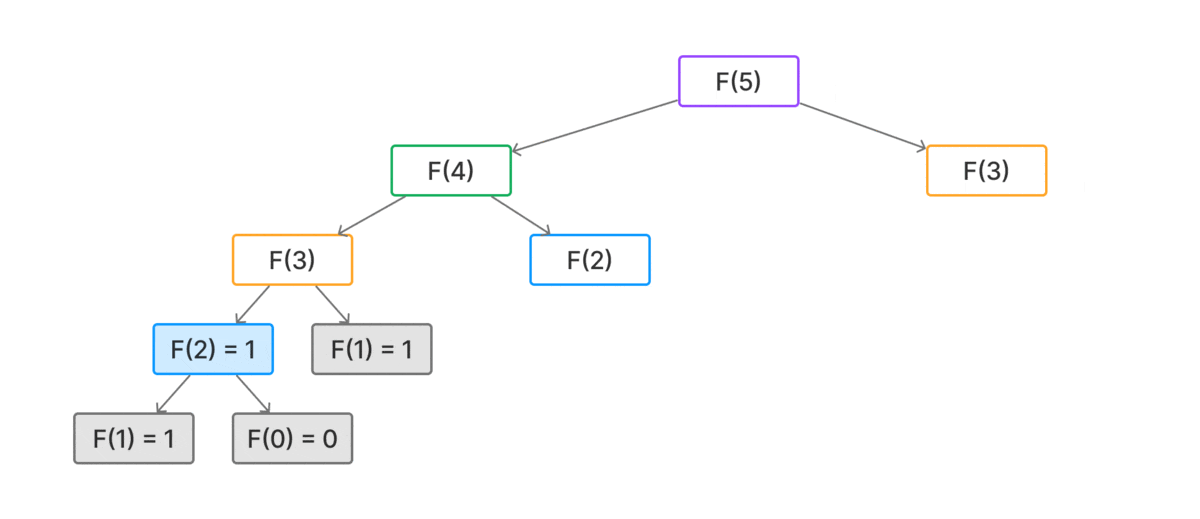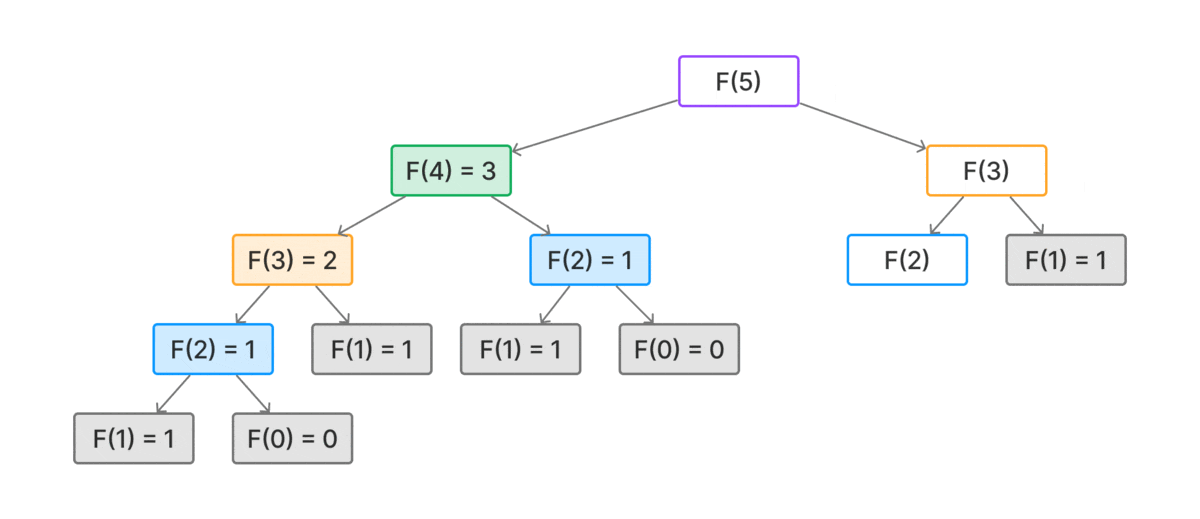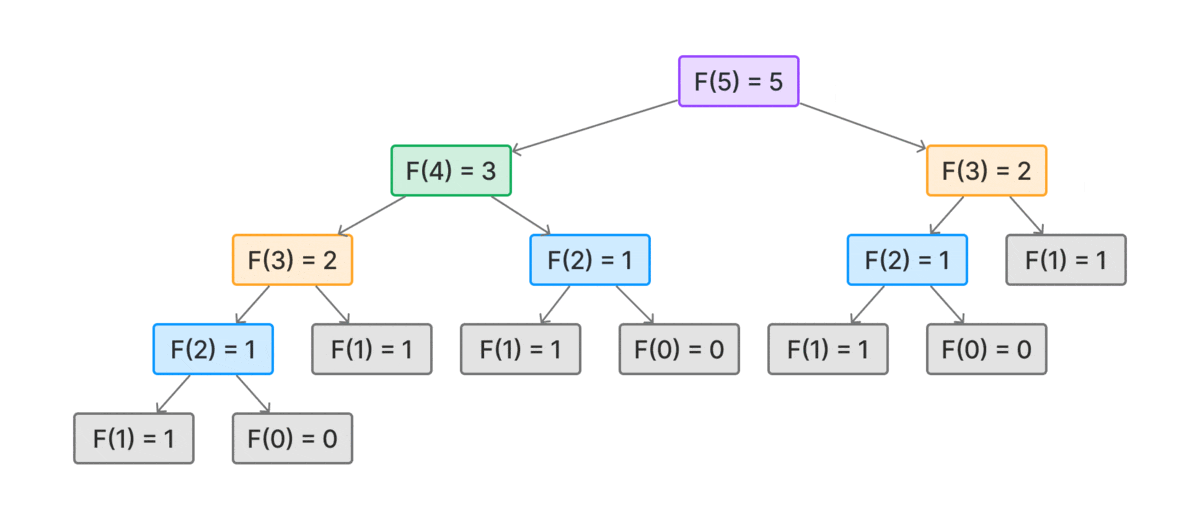
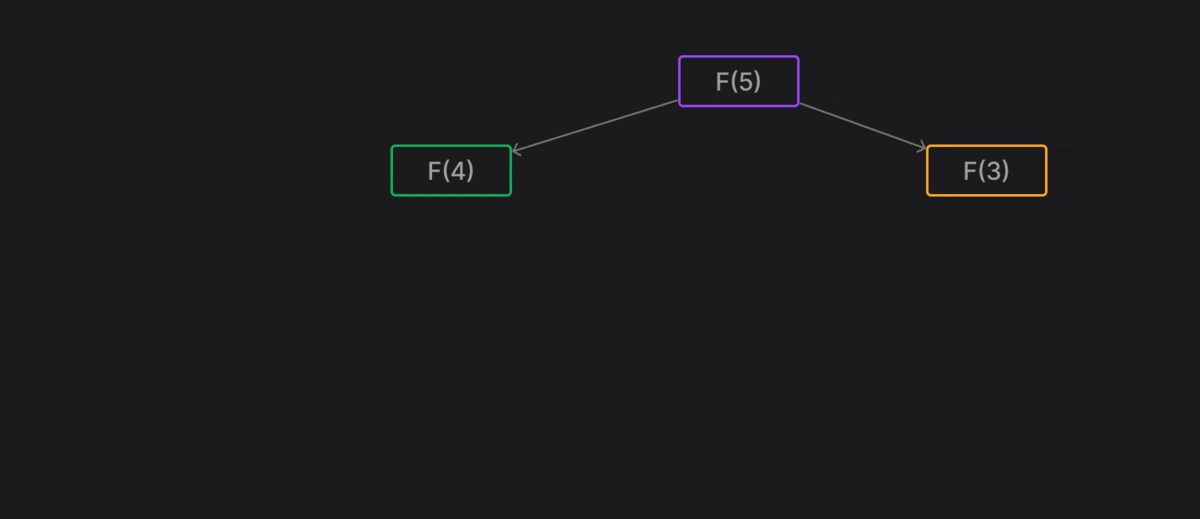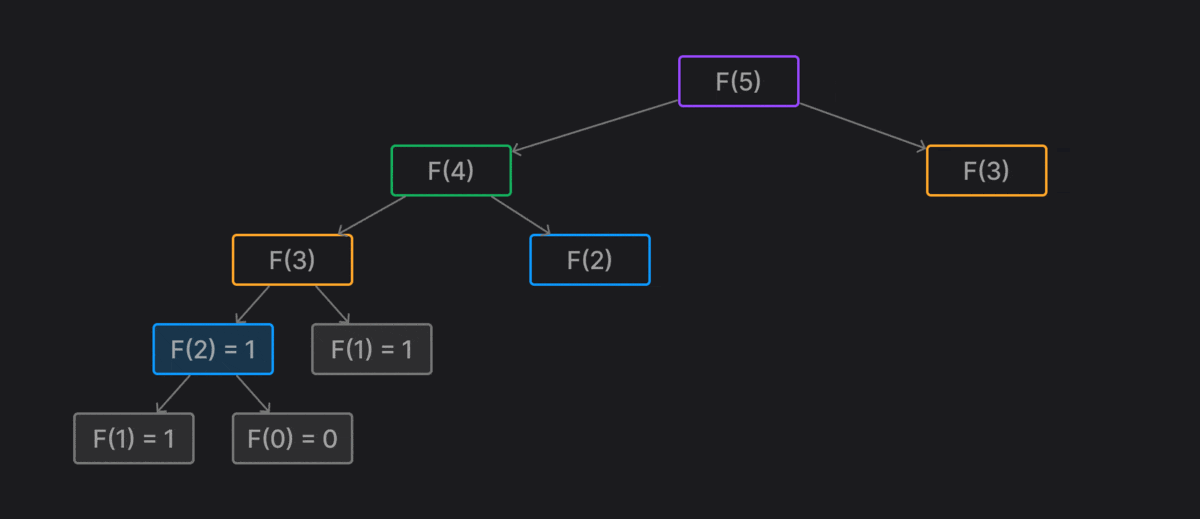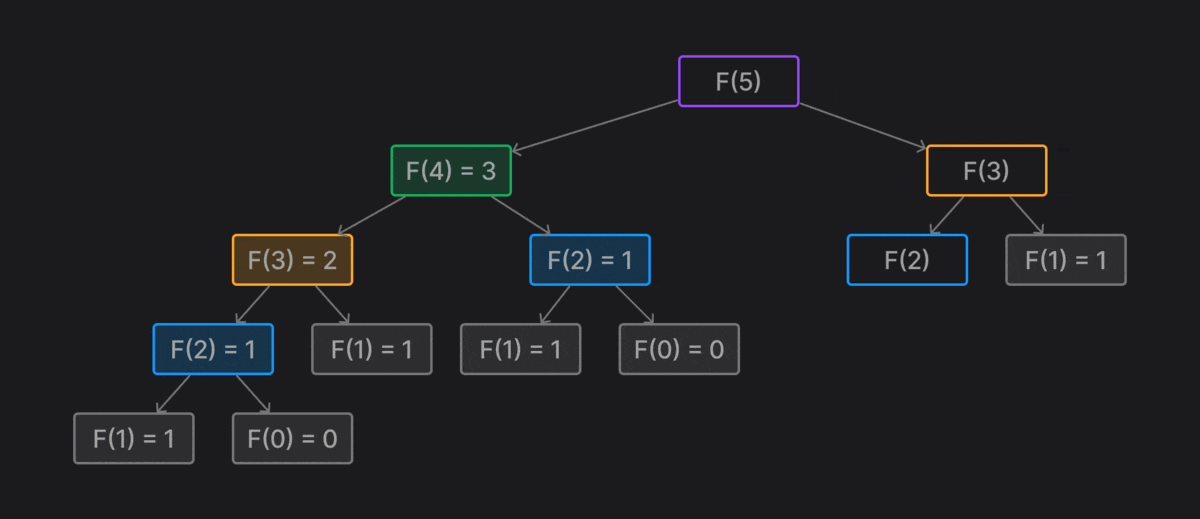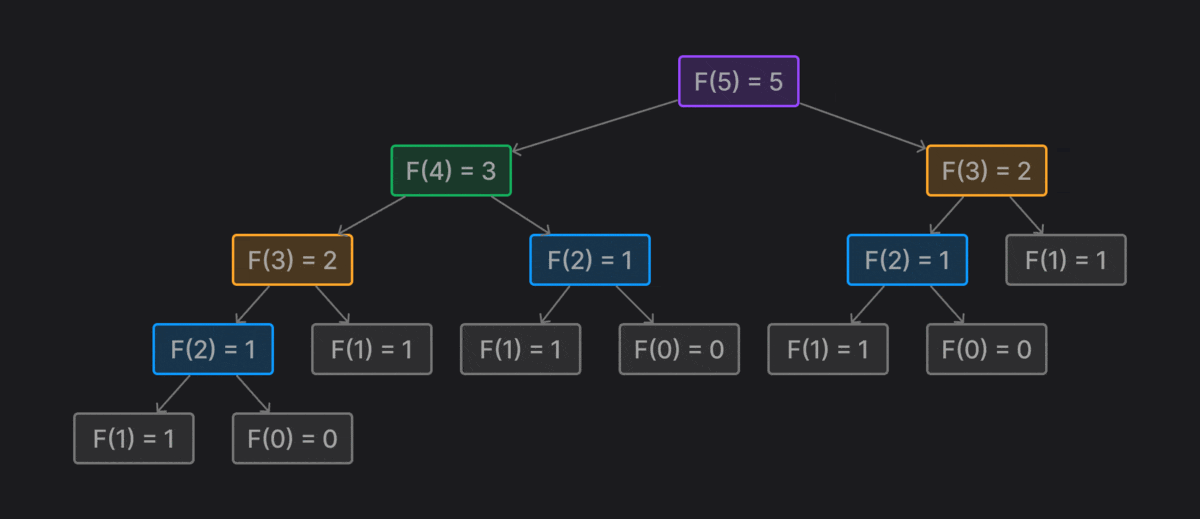
Tuy nhiên, cách làm này tốn rất nhiều tài nguyên của máy và bị lặp lại phép tính nhiều lần.
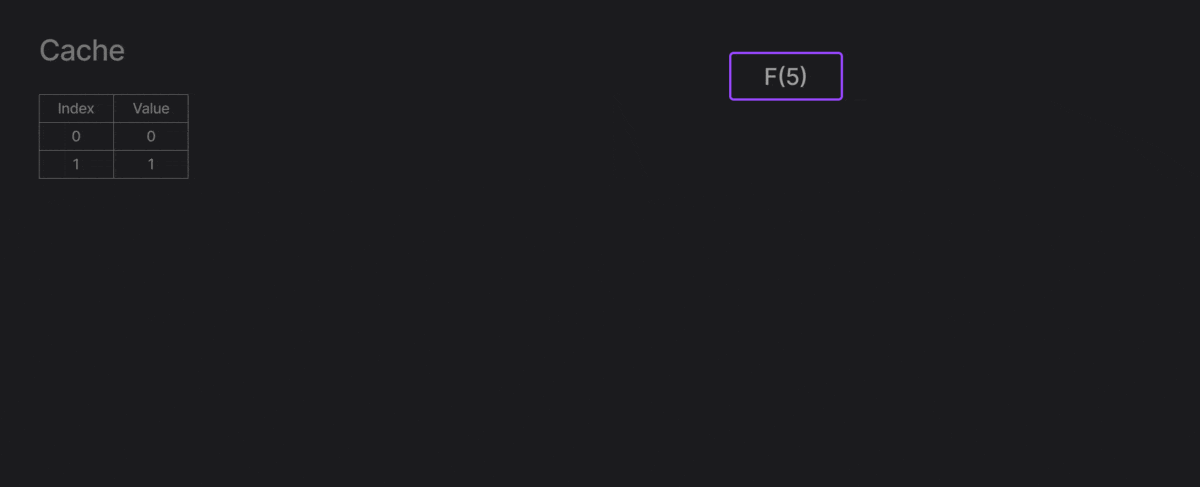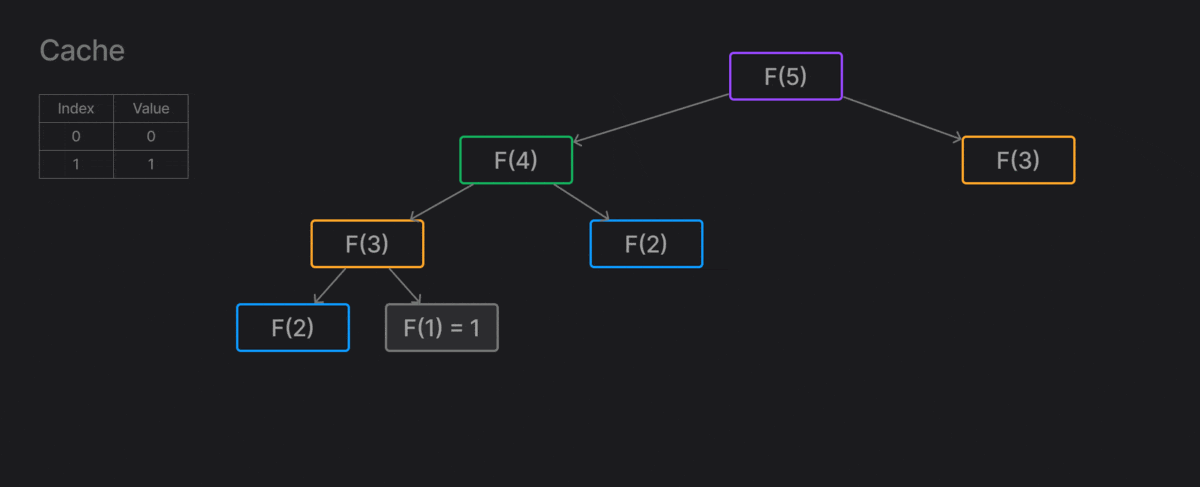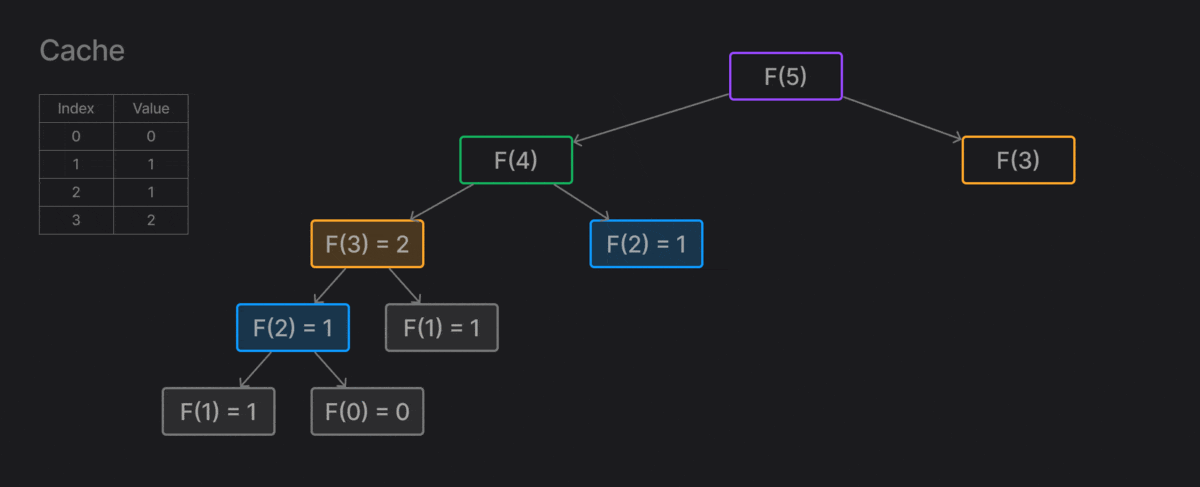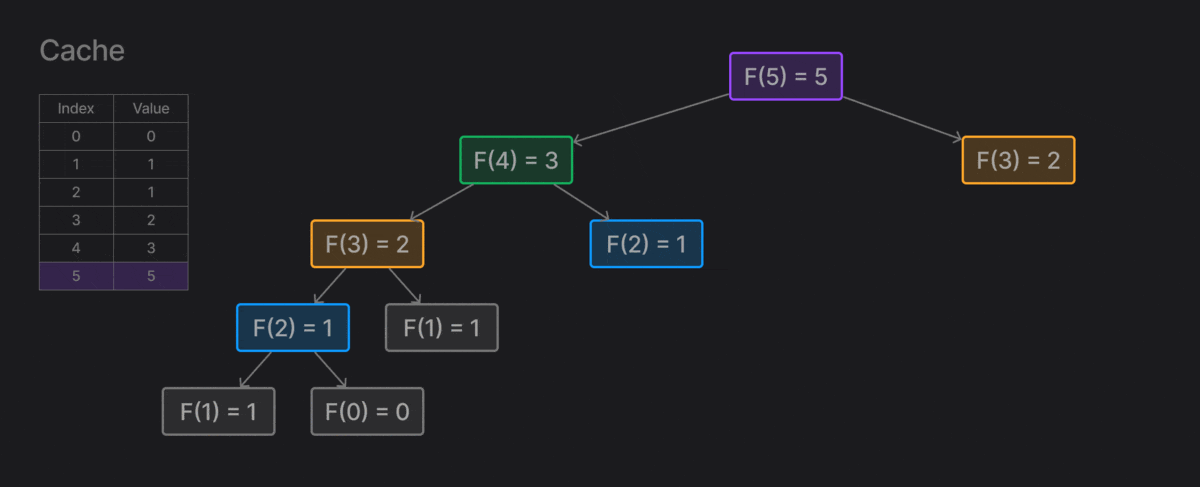
Ảnh động bên dưới sẽ miêu tả quá trình tính toán của thuật toán đệ quy
Cải tiến
Để cải thiện thuật toán, ta sẽ lưu trữ các giá trị đã tính toán, để tránh phải lặp lại nhiều lần.
Sau đây là code đệ quy tham khảo từ trang realpython.com
1
2
3
4
5
6
7
cache = {0: 0, 1: 1} # Tạo cache để lưu trữ, mặc định có F0=0, F1=1
def fibonacci_recursive(n: int) -> int:
if n in cache: # Kiểm tra xem vị trí này đã được tính chưa
return cache[n]
cache[n] = fibonacci_recursive(n-1) + fibonacci_recursive(n-2)
return cache[n]
Việc sử dụng hàm đệ quy để tính toán sẽ tạo ra rất nhiều vòng lặp, dẫn đến tình trạng tràn bộ nhớ
stack overflow, và đối với hàm này thì máy của mình không thể chạy được với n > 2933
Sử dụng ma trận
Dạng ma trận của số Fibonacci
Ta có thể tìm số Fibonacci tại vị trí n, $F_n$, trong phép tính sau:
\[\begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} ^ {n} = \begin{bmatrix} F_{n+1} & F_n \\ F_n & F_{n-1} \end{bmatrix}\]Để tìm $F_{n}$, ta có thể luỹ thừa ma trận \(\begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}\) đến bậc n. Nội dung bên dưới sẽ cố gắng chứng minh phương trình này trước khi đi vào code ứng dụng.
Chứng minh trực tiếp
Trước khi chứng minh phương trình, ta cần thống nhất rằng ở đây dãy số Fibonacci có thể mở rộng theo chiều âm. Từ phương trình:
\[F_{n+1} = F_{n} + F_{n-1}\]Ta có hệ phương trình như sau:
\[\begin{aligned} \begin{cases} F_{n+1} &= F_{n} + F_{n-1} \\ F_{n} &= F_{n} \end{cases} \end{aligned}\]Hệ phương trình này tương đương với phép tính ma trận sau:
\[\begin{aligned} \begin{bmatrix} F_{n+1} \\ F_{n} \end{bmatrix} &= \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} F_{n} \\ F_{n-1} \end{bmatrix} \\[1ex] &= \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} F_{n-1} \\ F_{n-2} \end{bmatrix} \\[1ex] &= \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} ^ {2} \begin{bmatrix} F_{n-1} \\ F_{n-2} \end{bmatrix} \\[1ex] &= \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} ^ {3} \begin{bmatrix} F_{n-2} \\ F_{n-3} \end{bmatrix} \\ &\dots \\ &= \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} ^ {n} \begin{bmatrix} F_{1} \\ F_{0} \end{bmatrix} \;\;\; (I) \\ \end{aligned}\]Tương tự ta cũng có:
\[\begin{bmatrix} F_{n} \\ F_{n-1} \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} ^ {n} \begin{bmatrix} F_{0} \\ F_{-1} \end{bmatrix} \;\;\; (II)\]Thay $F_{-1} = 1$, $F_{0} = 0$, $F_{1} = 1$ vào phương trình $(I)$ và $(II)$, ta có hệ:
\[\begin{aligned} \begin{cases} \begin{bmatrix} F_{n+1} \\ F_{n} \end{bmatrix} &= \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} ^ {n} \begin{bmatrix} 1 \\ 0 \end{bmatrix} \\[1ex] \begin{bmatrix} F_{n} \\ F_{n-1} \end{bmatrix} &= \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} ^ {n} \begin{bmatrix} 0 \\ 1 \end{bmatrix} \\ \end{cases} \end{aligned}\]Sử dụng tính chất sau:
\[\begin{cases} a = Mb \\ c = Md \end{cases} \implies \begin{bmatrix} a \\ c \end{bmatrix} = M \begin{bmatrix} b \\ d \end{bmatrix}\]Ta được:
\[\begin{bmatrix} F_{n+1} & F_{n} \\ F_{n} & F_{n-1} \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} ^ {n} \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} ^ {n}\]Sau khi tối giản ma trận đơn vị, ta có được phương trình cần chứng minh.
Chứng minh bằng quy nạp
Với $n = 1$, ta có:
\[\begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} = \begin{bmatrix} F_{2} & F_{1} \\ F_{1} & F_{0} \end{bmatrix}\]Giả sử mệnh đề đúng với với $n \geq 1 $, tức là:
\[\begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} ^ {n} = \begin{bmatrix} F_{n+1} & F_{n} \\ F_{n} & F_{n-1} \end{bmatrix}\]Ta cần chứng minh mệnh đề cũng đúng với $n+1$, xét:
\[\begin{align} \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} ^ {n+1} &= \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} ^ {n} \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \\[1ex] &= \begin{bmatrix} F_{n+1} & F_{n} \\ F_{n} & F_{n-1} \end{bmatrix} \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \\[1ex] &= \begin{bmatrix} F_{n+1} + F_{n} & F_{n+1} + 0 \\ F_{n} + F_{n-1} & F_{n} + 0 \end{bmatrix} \\[1ex] &= \begin{bmatrix} F_{n+2} & F_{n+1} \\ F_{n+1} & F_{n} \end{bmatrix} \end{align}\]Vậy mệnh đề đúng với mọi số nguyên n.
Thuật toán
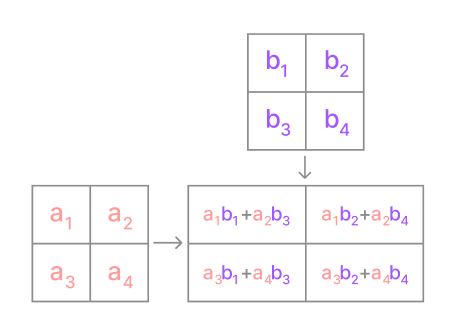
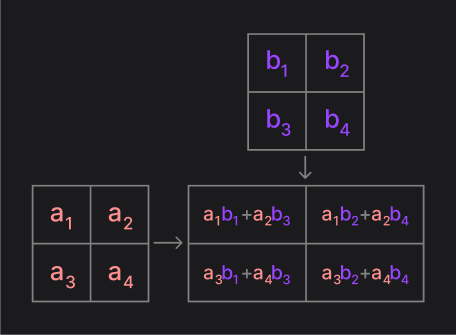
Phép nhân ma trận 2x2 được biểu diễn như sau
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def matrix_multiply(A, B):
# Ma trận nhập vào
[[a1, a2], [a3, a4]] = A
[[b1, b2], [b3, b4]] = B
return [ # Ma trận kết quả như hình minh họa
[a1*b1 + a2*b3, a1*b2 + a2*b4],
[a3*b1 + a4*b3, a3*b2 + a4*b4]
]
def matrix_power(input_matrix, n):
# Nếu mũ 0, trả về ma trận đơn vị
if n == 0:
return [[1, 0],
[0, 1]]
# Tính matrix^n
B = input_matrix
for power in range(2, n+1):
# Có thể viết gọn thành range(n-1)
# nhưng cần hiểu rằng ở đây đang tính từ mũ 2 đến mũ n
B = matrix_multiply(B, input_matrix)
print(power, B)
return B
def fibonacci_matrix(n):
input_matrix = [[1, 1],
[1, 0]]
result_matrix = matrix_power(input_matrix, n)
return result_matrix[0][1] # Hoặc result_matrix[1][0]
Sử dụng phương pháp fast doubling (tạm dịch tính nhanh bình phương)
Giới thiệu
Đây là thuật toán biến đổi từ thuật toán ma trận, nếu áp dụng công thức
\[\begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} ^ {n} = \begin{bmatrix} F_{n+1} & F_n \\ F_n & F_{n-1} \end{bmatrix}\]cho giá trị $n = 2.k$, ta có
\[\begin{align} (I) \begin{bmatrix} F_{2k+1} & F_{2k} \\ F_{2k} & F_{2k-1} \end{bmatrix} &= \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} ^ {2k} \\[1ex] &= \begin{bmatrix} F_{k+1} & F_k \\ F_k & F_{k-1} \end{bmatrix} ^ {2} \\[1ex] &= \begin{bmatrix} (F_{k+1})^2 + (F_k)^2 & F_{n+1}F_n + F_nF_{n-1}\\ F_nF_{n+1} + F_{n-1}F_n & (F_{k})^2 + (F_{n-1})^2 \end{bmatrix} (II) \end{align}\]Xét $(I) = (II)$ và áp dụng tính chất 2 ma trận bằng nhau, ta có hệ:
\[\begin{cases} \begin{align} F_{2k+1} &= (F_{k+1})^2 + (F_k)^2 \\ F_{2k} &= F_{n+1}F_n + F_nF_{n-1} \\ F_{2k-1} &= (F_{k})^2 + (F_{n-1})^2 \end{align} \end{cases} \\\]Với:
\[\begin{align} F_{2k} &= F_{k+1}F_k + F_kF_{k-1} \\ &= F_k (F_{k+1} + F_{k-1}) \\ &= F_k (F_{k+1} + (F_{k+1} - F_{k})) \\ &= F_k (2F_{k+1} - F_{k}) \\ \end{align}\]Vậy ta có hệ phương trình để tìm $F_n$ trong trường hợp n chẵn và lẻ:
\[\begin{cases} \begin{align} F_{2k} &= F_k (2F_{k+1} - F_{k}) \\ F_{2k+1} &= (F_{k+1})^2 + (F_k)^2 \end{align} \end{cases} \\\]Thuật toán
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def fd_method(n):
if n == 0:
return (0, 1)
a, b = fd_method(n//2) # a và b là giá trị F_k và F_k+1
c = a*(2*b - a) # c là F_2k
d = a*a + b*b # d là F_2k+1
if n % 2 == 0:
return (c, d)
else:
return (d, c+d)
def fibonacci_fast_doubling(n):
if n < 0:
raise ValueError("Cách này không áp dụng cho n < 0")
return fd_method(n)[0]
Mặc dù cũng sử dụng đệ quy để giải quyết bài toán, nhưng ở đây chúng ta xử lý theo cấp số nhân của 2. Vì thế thuật toán ít tình trạng bị stack overflow, không những thế còn chạy rất nhanh cho các số lớn.
So sánh các thuật toán
| Thuật toán | Thời gian chạy (Time complexity) | Bộ nhớ cần dùng (Space complexity) |
|---|---|---|
| Vòng lặp | O(n) | O(1) |
| Công thức Binet | O(1) | O(1) |
| Đệ quy | O(2^N) | O(N) |
| Đệ quy cải tiến | O(N) | O(N) |
| Ma trận | O(logN) | O(1) |
| Tính nhanh bình phương | O(logN) | O(N) |
Các nguồn tham khảo và mở rộng
- Websites:
- Algorithms for Competitive Programming: Fibonacci Numbers
- Art of Problems Solving: Binet Formula
- Geeks for Geeks: Nth Fibonacci Number
- Geeks for Geeks: Fast Doubling method to find the Nth Fibonacci number
- Math World: Fibonacci Number
- Math World: Fibonacci Q-Matrix
- Oran Looney: A Fairly Fast Fibonacci Function
- Project Nayuki: Fast Fibonacci algorithms
- Proof Wiki: Cassini’s Identity
- Wikipedia: Fibonacci Sequence
- Wikipedia: Generalizations of Fibonacci numbers
Hình ảnh được tạo bằng công cụ Figma
Ảnh động được tạo bằng công cụ ezgif.com